Анализ учебников

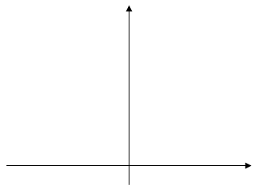
При любом х≠0 значения функции у=2х² больше соответствующего значения функции у=х² в 2 раза. Если переместить каждую точку графика функции у=х² вверх так, чтобы расстояние от точки до оси х увеличилось в 2 раза, то она перейдет в точку графика функции у= 2х², при этом каждая точка графика может быть получена из некоторой точки графика функции у=х². То есть, график функции у=2х² можно получить из параболы у=х² растяжением от оси х в 2 раза (рис.1).

Построим график функции у=х² по таблице значений:

При любом х≠0 значение функций у= х² меньше соответствующего значения функции у= х² в 2 раза.

Рассуждая аналогично предыдущему преобразованию авторы приходят к выводу, что график функции у= х² можно получить из параболы у= х² сжатием к оси х в 2 раза.

Вообще график функции у=ах² можно получить из параболы у= х² растяжением от оси х в а раз, если а>1, и сжатием к оси х в раз, если 0<а<1.

Симметрия относительно оси х рассматривается на примере сравнения графиков функций у= х² и у= -х².

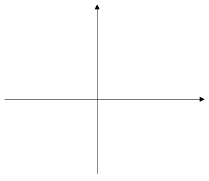
При любом х значение этих функций являются противоположными числами. Значит, соответствующие точки графиков симметричны относительно оси х. То есть, график функции у=-х² может быть получен из графика функции у=х² с помощью симметрии относительно оси х.

Вообще графики функций у=ах² и у=-ах² (при а≠0) симметричны относительно оси х.

В конце каждого пункта авторы предлагают выводы:

-график функции у= -f(х) можно получить из графика функции у= -f(х) с помощью симметрии относительно оси х;

-график функции у= аf(х) можно получить из графика функции у= f(х) с помощью растяжения от оси х в а раз, если а>1, и с помощью сжатия к оси х в раз, если 0<a<1.

Новое в образовании:

Трудности формирования навыков самообслуживания у детей из неблагополучных семей
Неблагополучная семья – это семья, в которой ребенок испытывает дискомфорт, стресс, пренебрежение со стороны взрослых, подвергается насилию или жестокому обращению. Главной характеристикой такой семьи является отсутствие любви к ребенку, заботы о нем, удовлетворения его нужд, защиты его прав и зако ...

Диагностика уровня конфликтности у детей старшего дошкольного возраста
Для исследования конфликтов дошкольников со сверстниками на базе МДОУ ЦРР д/с №19 города Ишима был проведен эксперимент. В эксперименте приняли участие дети старшей группы в количестве 20 человек. Они были поделены на две группы: экспериментальную и контрольную (по 10 человек в каждой). Эксперимент ...

Опытно-экспериментальная работа по воспитанию у детей положительных взаимоотношеий через совместную деятельность
В исследовании участвовали дети подготовительной к школе группы «АБВГДэйка» в количестве 15 человек. Контрольной группой была определена подготовительная к школе группа «Улыбка». Исследование проходило в 3 этапа: 1 этап констатирующий – сентябрь 2010г. 2 этап формирующий – октябрь 2010г. – март 201 ...